Vykonali sme niekoľko pokusov, pri ktorých sme skúmali, aká minimálna sila musí pôsobiť na teleso ležiace na vodorovnej podložke, aby sa pohlo a aká sila naň musí pôsobiť, ak je v pohybe, aby sa pohybovalo rovnomerne priamočiaro.
Zistili sme:
- Veľkosť prvej sily je väčšia než druhej
- Veľkosť oboch síl závisí od materiálov podložky a trecej plochy telesa. Kváder, ktorý mal steny z troch povrchov ( drevo, koža a oceľ) sa po laboratórnom stole najľahšie pohyboval na oceľovej strane a najťažšie na koženej strane. (Poznámka: Tento pokus sme robili v inej triede minulý rok, neviem nájsť ten kváder)
- Koľkokrát sa zväčší hmotnosť telesa, toľkokrát sa zväčší sila, ktorá musí pôsobiť, aby sa teleso pohlo, alebo, ak je v pohybe, konalo rovnomerný priamočiary pohyb. (Meranie ste robili vo viacerých skupinách, väčšine skupín vyšla takáto závislosť, niektoré namerali čosi iné, ale u všetkých sila rástla s hmotnosťou)
- Trecia sila nezávisí od veľkosti trecej plochy (pokiaľ tlak nie je priveľký a nie sú prekročené medze pevnosti materiálu, text vyznačený kurzívou sme nedokázali, je to moje, zatiaľ pokusom nepotvrdené tvrdenie a v literatúre sa táto samozrejmosť (?) obvykle nepíše).
- Toto sme nezistili, ale pokusmi by sme zistiť mohli: Sila šmykového trenia pre malé rýchlosti, nezávisí od rýchlosti, ktorou sa teleso pohybuje.
Sila, ktorú sme merali, nazývame trecia sila a tento fyzikálny jav nazývame trenie. Trenie v pokoji je pokojové trenie, trenie v pohybe je šmykové trenie.
Pokojové trenie sa tiež nazýva statické trenie. Šmykové trenie sa tiež nazýva dynamické alebo klzné trenie.
Maximálna sila pokojového trenia 
je:
kde 
je koeficient pokojového trenia a 
je kolmá tlaková sila medzi telesami (Normála je iný názov pre kolmicu, preto koeficient n, na prevzatých obrázkoch sa môže vyskytnúť koeficient N).
Sila šmykového trenia je
kde 
je koeficient šmykového trenia.
Koeficient pokojového trenia je bezrozmerná fyzikálna veličina, ktorá udáva pomer maximálnej trecej sily a kolmej tlakovej sily pri pokojovom trení. 
Koeficient šmykového trenia je bezrozmerná fyzikálna veličina, ktorá udáva pomer trecej sily a kolmej tlakovej sily pri šmykovom trení. 
V literatúre sa tiež môžno stretnúť s termínom súčiniteľ pokojového/šmykového trenia a môžete sa stretnúť so značkou pre koeficient trenia 
(grécke písmeno mí).
| Látka 1 | Látka 2 | Koeficient pokojového trenia |
Koeficient kĺzavého trenia |
|
|---|---|---|---|---|
| Oceľ | Oceľ | 0.4 | 0.1 | |
| Oceľ | Drevo | 0.55 | 0.35 | |
| Oceľ | Ľad | – | 0.027 | |
| Drevo | Drevo | 0.65 | 0.3 | |
| Drevo | Ľad | – | 0.0035 | |
| Drevo | Koža | 0.47 | 0.27 | |
| Guma | Ľad | 0.1-0.2 | – | |
| Guma | Suchý asfalt | 0.55 | – | |
| Guma | Mokrý asfalt | 0.2-0.5 | 0.2 |
Zdroj: Matematické, fyzikálne a chemické tabuľky pre stredné školy. SPN Bratislava, 1989 ISBN 80-08-00050-3
Meranie koeficientu trenia
Koeficient pokojového trenia sme odmerali a vypočítali dvoma spôsobmi.
Prvý spôsob merania spočíval v tom, že sme zväčšovali silu vo vodorovnom smere a medznú silu, pri ktorej sa teleso začalo pohybovať, sme pokladali za maximálnu treciu silu pokojového trenia. Veľkosť tejto sily sme určili do istej miery odhadom, vedeli sme určiť iba sily, pri ktorých sa teleso ešte nehýbalo.
Druhý spôsob merania spočíval v tom, že sme teleso položili na naklonenú rovinu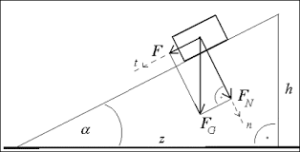 
a postupne sme zväčšovali jej sklon. Pri istom medznom sklone sa teleso pohlo. Koeficient pokojového trenia sme vypočítali z rozmerov naklonenej roviny.
Trojuholníky so stranami 
sú si podobné (l je dĺžka naklonenej roviny, na obrázku nie je označená). Potom platí 
. Keďže zároveň platí 
, dostaneme vzťah (3a).
Z toho dostaneme vzťah:
Ak by ste preberali goniometrické funkcie, vedeli by ste, že (3b) zodpovedá goniometrickej funkcii tangens.
Aj pri tomto spôsobe merania koeficientu statického trenia ho do istej miery určíme odhadom, ale miera chyby je výrazne menšia než pri prvom spôsobe (Zdôvodnite prečo!).
Otázka
Ktorý koeficient trenia možno vypočítať, ak naklonená rovina má väčší než je medzný sklon pre statické trenie a odmeriame silu, ktorá pôsobí na silomer, keď je teleso v pokoji?
a) statický b) dynamický c) žiaden z nich d) oba
Odpoveď zdôvodnite. Ak je to a) alebo b) alebo d) odvoďte vzorec pre výpočet príslušného koeficientu.
Oba koeficienty môžeme merať horizontálnym drsnomerom.
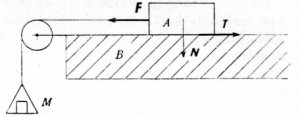
Odmeriame hmotnosť telesa A, na misku M postupne pridávame závažia, keď prekročíme medznú hodnotu, teleso sa začne kĺzať rovnomerne zrýchleným pohybom, posledne pridané závažie odoberieme a pridáme ľahšie závažie. Postupujeme tak dlho, ako nám dovoľuje najmenšie závažie, ktoré máme k dispozícii. Silu F vypočítame z gravitačného zrýchlenia. Keďže chceme zistiť koeficient f, na gravitačnom zrýchlení, ak je nenulové, nezáleží. Stačí odmerať hmotnosť kvádra a spočítať hmotnosť závaží 
Koeficient šmykového trenia by sme určili rovnako, len by sme kvádrom navyše pohli a hľadali by sme hmotnosť, pri ktorej sa bude kváder pohybovať rovnomerným priamočiarym pohybom.
Meranie koeficientu kĺzavého trenia
Kĺzavé trenie sme merali tak, že sme zmerali silu, pri ktorej sa teleso šmýkalo rovnomerným priamočiarym pohybom. Meranie bolo pomerne nepresné, keďže teleso sme ťahali rukou a nevedeli sme zaistiť, aby šlo skutočne o rovnomerný priamočiary pohyb, tiež sme nemali istotu, či pôsobíme silou, ktorá je rovnobežná s plochou, po ktorej sa teleso kĺzalo.
Keď je teleso v pohybe a pohybuje sa po vodorovnej podložke, po nejakom čase sa zastaví, lebo naň pôsobí trecia sila kĺzavého trenia. Zo správania sa pohybujúceho sa telesa môžeme určiť veľkosť koeficientu kĺzavého trenia. Pokiaľ naopak poznáme koeficient kĺzavého trenia, z veľkosti prejdenej dráhy telesa môžeme vypočítať jeho počiatočnú rýchlosť a ak poznáme počiatočnú rýchlosť a koeficient trenia, vieme vypočítať brzdnú dráhu telesa.
Koeficient šmykového trenia môžeme zmerať a vypočítať tiež nasledujúcimi pokusmi.
Pokus 1
Teleso položme na naklonenú rovinu, ktorá má väčší sklon, než je medzný sklon pre statické trenie. Odmeriame dĺžku naklonenenej roviny a čas, za ktorý teleso prejde naklonenenou rovinou z pokojovej rýchlosti.
Odvoďte vzťah, ktorým možno vypočítať f.
Pokus 2
Na vodorovnej ploche podobným spôsobom určíme f tak, že na teleso motúzom pripevníme závažie, pričom závažie bude mať takú hmotnosť, že sa teleso začne pohybovať rovnomerne zrýchleným pohybom, motúz povedieme cez koliesko na oske, aby sme minimalizovali iné trenia, mimo trenia telesa o podložku. Odmeriame hmotnosť telesa m, hmotnosť závažia 
, dráhu s po ktorej sa bude teleso pohybovať a čas t, za ktorý túto dráhu prejde. Pokladajme gravitačné zrýchlenie 
Odvoďte vzťah, ktorým možno vypočítať f.
Je trenie užitočné alebo škodlivé?
Vo všeobecnosti je trenie užitočné, ak by nebolo trenia, takmer by sme sa nevedeli pohybovať, nevedeli by sme si zaviazať šnúrky na topánkach, nefungovalo by spájanie klincami ani šrúbami, nevedeli by sme sa z pokoja pohnúť, ak by sme boli v pohybe, nevedeli by sme sa zastaviť. Keď je poľadovica, výrazne stúpa počet dopravných nehôd, ako aj úrazov chodcov. Časté sú aj prípady, kedy chceme trenie minimalizovať, inak musíme na tú istú činnosť vynaložiť výrazne viac práce, než keď je trenie zanedbateľné. Trenie môžeme znížiť vhodnou voľbou látok, ktoré sa o seba trú a mazaním. Tiež ho môžeme znížiť tým, že kĺzavé trenie nahradíme valivým trením – preberieme niekedy nabudúce.
Zvýšenie trenia dosiahneme znova vhodnou voľbou materiálov. V zime napríklad posypujeme zľadovatelé chodníky pieskom, štrkom alebo popolom. Keď brzdíme, mali by sme sa snažiť brziť tak, aby po celý čas išo o statické trenie a nie o trenie v šmyku (Prečo?).
Otázky
- Ako by mal vodič brzdiť. ak má byť brzdná dráha čo najkratšia?
- Ako funguje ABS?
- Je pri ABS vždy brzdná dráha kratšia než bez neho? Ak je niekedy brzdná dráha s ABS dlhšia(?), je jazda aj vtedy bezpečnejšia? Zdôvodni prečo je, či prečo nie je.